Electrophoresis Buffers–The Henderson-Hasselbalch Equation
In its simplest form, a buffered solution contains a mixture of a weak acid and its conjugate base.
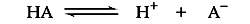
The position of acid/base equilibrium is represented by the acid dissociation constant, Ka. This number is large if the acid is stronger and equilibrium tends toward dissociation. It is small for an equilibrium that tends toward proton capture. Buffers used in life science tend to range from 10-4 to 10-10 in their Ka values.
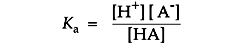
Ka is usually expressed as its negative logarithm, pKa:
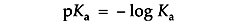
A buffer with a Ka of 10-2 has a pKa of 2, favoring dissociation. A buffer with a Ka of 10-12 has a pKa of 12, favoring proton capture.
After a few math operations, the expression for the dissociation quotient becomes a very useful form, the Henderson-Hasselbalch equation:
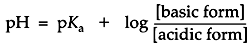
This equation is central to buffer design. The formula states that the pH of a buffered solution will differ from the buffer's pKa by an amount which is determined by the ratio of the base to the acid forms in the solution. If these concentrations are equal then the pH = pKa. If the concentration of the base form is greater than the acid then the pH is greater than pKa. If the concentration of acid form is greater than the base then pH is less than pKa.
A buffer maintains a nearly constant pH by absorbing protons released by other sources in solution or releasing protons if another species is depleting them. For example, a small amount of strong acid introduced to pure water causes the pH to plummet five or six points. However, if that same amount of strong acid were introduced to a concentrated buffer solution, it merely causes the change of some of the buffer's weak base form to the weak acid form. By the Henderson-Hasselbalch equation, to drop the pH of the solution a full point below the pKa, enough base would have to be consumed for the concentration of the acid form to become ten times greater than the base. If the buffer is sufficiently concentrated, the small amount of strong acid in this example would barely alter the pH. In electrophoresis, the buffer is able to maintain a relatively constant pH as long as neither the acid nor the base becomes exhausted.
The Henderson-Hasselbalch equation gives information in addition to how the pH is a function of the relative predominance of acid-base forms of a buffer. For certain instances, it is useful to think of this equation the other way around. In predicting the state of ionization of minor solution components, for example, it can be useful to think of the relative predominance of various forms as a function of an externally determined pH. An instructive example might be a solution whose pH is maintained by a concentrated buffer. The degree of ionization of a minor component in this solution, such as a protein, would depend on the pH of its environment, determined by the buffer. Suppose an ionizable group upon a protein has a pKaof 11, an amine group, for example, which might be either the nonionized amine form (base) or the ammonium ion form (acid). If the solution is buffered to a stable pH of 8, the Henderson-Hasselbalch equation tells you that the ammonium ion form will predominate at a ratio of 1000 to 1. In native protein electrophoresis, this concept is essential to understanding how buffers control the state of ionization of sample molecules.
NEXT TOPIC: Choosing the Right Electrophoresis Buffer
